数据结构

复杂度

大O表示法

时间复杂度

算法执行时间随输入规模增长而变化的度量

空间复杂度

空间随输入规模增长而变化的度量（输入数据不算空间）

渐进符号（看不懂，后面再看）

分为三个界~~（这不华为么）~~

上界O 下界Ω 紧致界θ

例如，判断10n^2 + 4n + 2 = O(n^2)是否成立

则上界的括号里面需要大于等于表达式的复杂度

下界 需要 小于等于

紧致界 需要 等于

递归时间、空间复杂度

• 时间复杂度：递归的次数 * 每次递归的时间复杂度

• 主观法（从Spike8086处学习）：

  

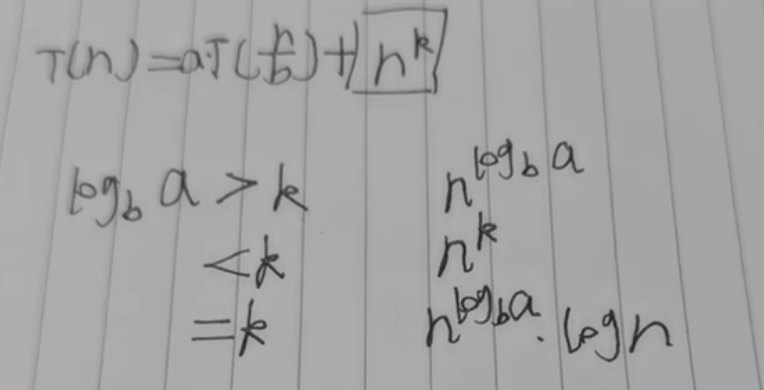
  这里的T(n/b)是和T(n)类似的函数！！

  常见题目是

  1. 计算空间复杂度。
     1. 符合上面公式的直接套。
     2. n^k对不上而且有㏒^kn的，直接选有㏒^k+1n的
  2. 两个算法比速度，求算式中某个值的最大值。
     1. 套到公式里，使得两个的值尽量靠近

线性结构

线性表

• 顺序储存 ｜ 链式储存

顺序存储

• 使用地址连续的储存单元依次存储线性表
• 插入：先移动元素、再加入添加的元素。
  • 长度为n，期望为n / 2
  • 最好：O(1)
  • 最坏：O(n)
  • 平均（同上面期望）：O(n)
• 删除：先删除元素，再移动剩余元素。
  • 长度为n，期望为(n - 1) / 2
  • 最好：O(1)
  • 最坏：O(n)
  • 平均（同上面期望）：O(n)
• 查找：O(1)

链式存储

• 通过指针链接起来的结点来存储数据元素。[数据域, 指针域]
• 插入：新node.next指向prev.next，prev.next再指向node
  • 最好：O(1)
  • 最坏：O(n)
  • 平均：O(n)
• 删除：prev.next指向prev.next.next
  • 最好：O(1)
  • 最坏：O(n)
  • 平均：O(n)
• 查找：循环查找next
  • 最好：O(1)
  • 最坏：O(n)
  • 平均：O(n)

循环单链表

• 可以从任何一个结点开始，遍历完整个数据结构。
• 尾结点：表的最后一个结点，尾部插入时可以直接用尾结点进行操作。

双链表

• [数据域, 指针域（前、后）]

栈

• 只能访问数据结构的一端，先进后出、后进先出
• 栈的链式存储，只需要设置栈顶指针。入栈、出栈都不需要遍历链表。
• 常用于实现函数或过程的递归调用及返回处理时
• 做题时切记，给的元素可以单个进了就出，不是非要所有一起进！！

队列

• 先进先出的线性表，插入端称为队尾，删除端称为队头。
• 插入、删除后，之前的空间无法再利用，所以出现了循环队列，尾指针是在最后的元素后面一个位置。

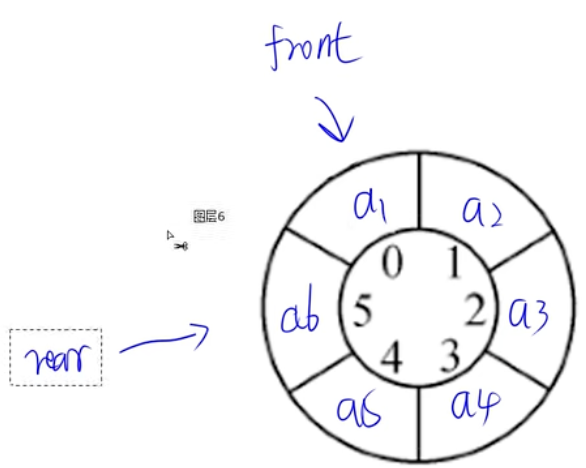
• 队列链式存储（队头、队尾指针）
• 双端队列：两端都可以入或出（根据题目来定）

📒 从题中的总结

• 采用循环队列的优点是：入队出队操作都不需要移动队列中其他元素。（静态队列需要移动，避免之前用过的空间无法再使用）
• 两个栈可以模拟一个队列

串

• 是特殊的线性表，仅由字符构成的有限序列。

串的模式匹配

• 模式串m去主串n中进行匹配
• 朴素模式：一个一个去对比，去暴力对比。
  • 复杂度最好：O(m)
  • 最坏：m * (n - m + 1) = O(n * m)
  • 平均：O(n + m)
• KMP
  • 串的前缀：包含第一个字符且不含最后一个字符的子串
  • 串的后缀：包含最后一个字符且不含第一个字符的子串
  • 第i个字符的next值：从1到i - 1串中最长相等前后缀长度 + 1。其中，next[1] = 0
  • KMP算法
    • 主串i，模式串j，对比时i不回退
    • 当不匹配时，j回到next值，并和i进行比较

数组

• 二维数组：a[行号][列号]

• 行存储：优先铺满行；列存储：优先铺满列

  

矩阵（题目进行带入验证）

• 对称矩阵
  • 储存下三角区 + 对角线元素。
  • a[i, j] = a[j, i]
• 三对角矩阵
  • 主对角线附近的元素有值
• 稀疏矩阵
  • 非常多的0元素，将其储存为一维数组，每个元素包含[行号, 列号, 值]
  • 压缩存储方式为 三元组顺序表 和 十字链表

树

• 非线性结构，一个数据元素可有0个或多个直接后继元素
• 概念：
  • 双亲：父结点
  • 结点的度：结点的子树个数
  • 叶子结点：度为0的结点
  • 内部结点：度不为0的结点
  • 结点的层次：字面意思。
  • 树的高度：一个树的最大层树为树的高度
• 性质：
  • 树中结点总数等于所有结点的度数之和加一（根结点）
  • 度为m的树中，第i层最多有m^i-1个结点
  • 高度为h的m次树（度为m），最多有(m ^ h - 1) / (m-1)个结点
  • 具有n个结点，度为m的树的最小高度为logm(n*(m-1) + 1)

二叉树

• 二叉树中结点的子树要区分左、右子树，即使只有一棵子树，也要指明是左还是右。
• 性质（大部分由上面树的性质推出）：
  • 对于任意一棵二叉树，度为0的结点数等于度为2的结点数+1
• 满二叉树：深度为k的二叉树有2^k-1个结点。有n层，则除了第n层全是度为2的结点，最满的情况！！
• 完全二叉树：在满二叉树的基础上，最后一层可不满，但是都是从左往右排列。
  • 具有n个结点的完全二叉树的高度为Math.floor(log₂n) + 1或Math.ceil(log₂(n+1))

存储结构

• 顺序存储（做题现画现推）

  • 中序遍历后依次存入，空结点也要存入。
  • 最坏情况下深度为k且只有k个结点的二叉树，需要2^k-1个存储单元

• 链式存储

  • 二叉链表储存左右子结点的指针

  

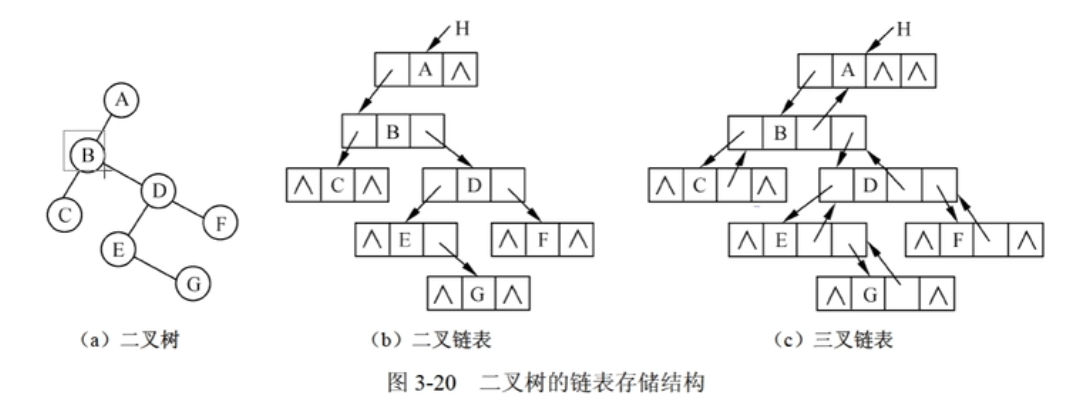
📒 从题中的总结

• 完全二叉树更适合顺序存储，空结点少，利用率高
• 计算链表存储二叉树时，空指针记得计算根结点！！

二叉树的遍历

• 先序遍历：根 ➡️ 左 ➡️ 右
• 中序遍历：左 ➡️ 根 ➡️ 右
• 后序遍历：左 ➡️ 右 ➡️ 根
• 层序遍历：从上往下，从左到右遍历
• 给出序列（一定有中序），反向构建二叉树：
  • 先序：可以立刻确定第一个为根结点
  • 后序：可以立刻确定最后一个为根结点
  • 层序：第一个为根结点
  • 根据先、后去确定根结点，分左右后再次确定下面的根结点

平衡二叉树

• 二叉树中任意一个结点的左右子树高度之差绝对值不超过1

二叉排序树（左边小，右边大）

• 结点的值 大于左子树所有结点的值；小区右子树所有结点的值。
• 通过中序遍历得到的序列是有序序列
• 二叉排序树的构造：依次比较，小则作为左树，大则作为右树
• 效率最差的二叉查找树是：单只树
• 从左到右排列同层次的结点，其关键字呈现有序排列的特点

最优二叉树（哈夫曼树）

• 加权路径长度最短的树。加权：结点的值 * 到结点的路径

• 构造哈夫曼树（给出权值）：以1 3 3 4为例

  • 选出最小的两个值（1、3），以这两个作为子结点
  • 生成父结点，值为1+3=4，现在权值为 4 3 4
  • 同上，再选（4、3）作为子结点
  • 生成父结点4+3=7，现在权值为 7 4
  

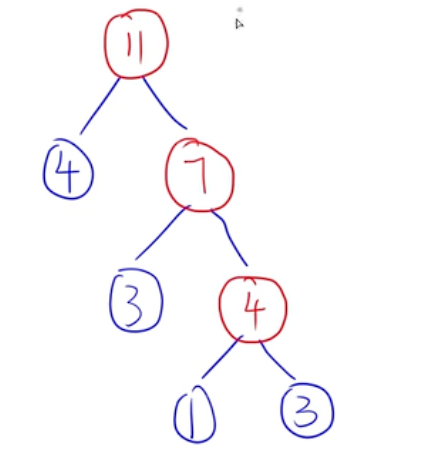
• 构造规则：

  • 从前往后找权值最小
  • 小左大右
  • 相加后加入末尾
  • 权值相同，从前往后找

• 哈夫曼编码：先编码，再组树，再通过路径编码

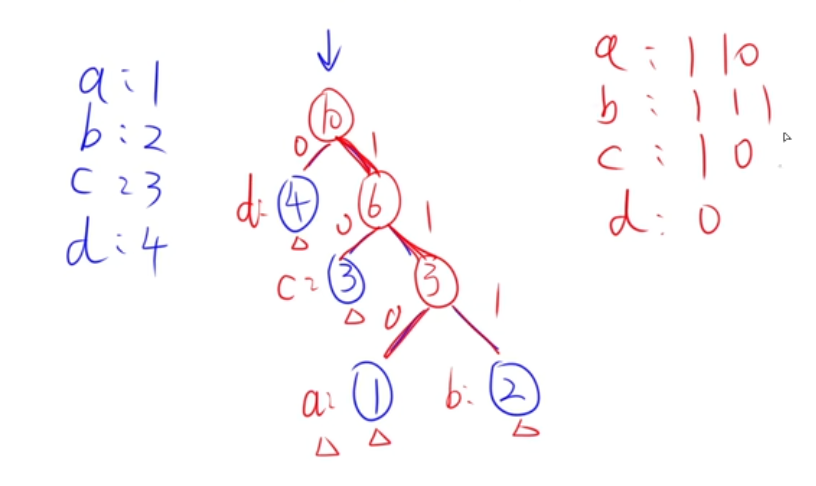
• 哈夫曼编码压缩比
  • 先算等长编码：2^n >= 字符数
  • （等长 - 压缩） / 等长

📒 从题中的总结

• 哈夫曼编码方案基于 贪心策略
• 哈夫曼权重越大离根越近，权重越小离根越远

线索二叉树

• 利用结点的空指针域来存放结点的前驱、后继信息。

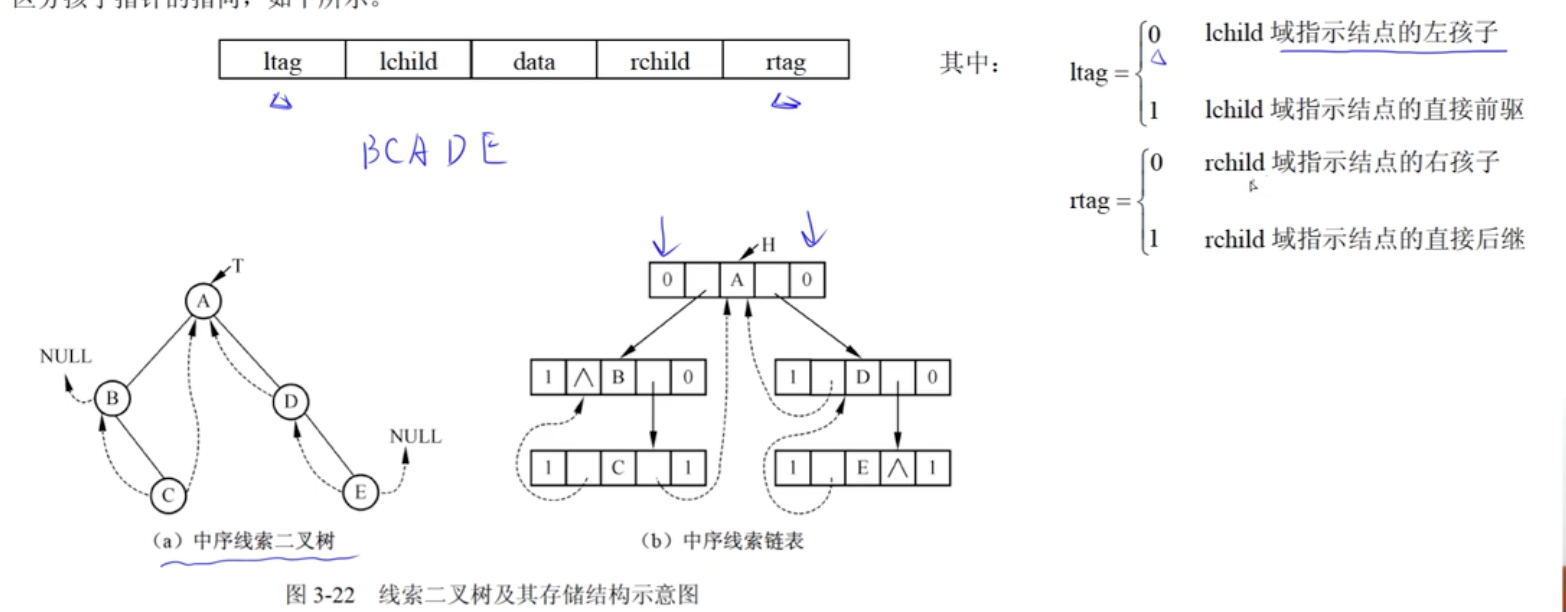
图

• 任意两个结点之间都可能有直接的关系。

图的定义

• G=(V,E)，V是顶点的非空集合，E是图中边的有限集合

有向图

• 图中每条边都是有方向的，顶点之间用<vi,vj>表示，vi为起点

无向图

• 图中每条边都是无方向的，<vi,vj>和vj,vi是一样的

完全图

• 每个点都连接了其他点。
• n个顶点的无向完全图共有n * (n - 1) / 2条边。
• n个顶点的有向完全图共有n * (n - 1)条边。

度

• 顶点的度是关联于该顶点的边的数量，记作D(v)。
• 有向图的度 = 出度 + 入度

路径

• 由边组成，由一个顶点到另一个顶点
• 第一个顶点和最后个顶点相同的路径称为 回路或环
• 简单路径：从一个顶点到另一个顶点，所有顶点都不重复。

连通图、连通分量（针对无向图）

• 顶点A、B之间有路径（不是一定要直连），称AB连通
• 图中任意两个顶点都是连通的，图为连通图
• n个顶点最少有n-1条边即可成为连通图

强连通图、强连通分量（针对有向图）

• 同上，只是带了方向
• n个顶点最少有n条边即可成为连通图

图的存储结构

邻接矩阵表示法

• 对于n个顶点的图，邻接矩阵是个n阶方阵。其中A[i][j]表示(vi,vj)是边（用1、0表示）
• 无向图的邻接矩阵是对称的。

邻接链表表示法

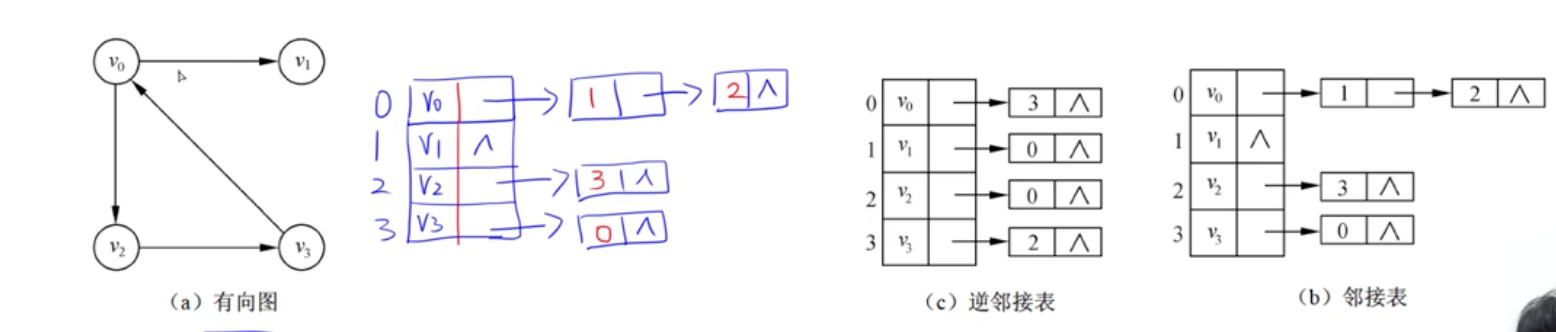
稠密图、稀疏图

• 稠密图：边多，适合邻接矩阵
• 稀疏图：边少，适合邻接表

图的遍历

• 深度优先搜索DFS（同树）
  • 矩阵复杂度O(n ^ 2)
  • 链表O(n + e)，n为顶点，e为边
• 广度优先搜索DFS（同树） 使用队列
  • 矩阵复杂度O(n ^ 2)
  • 链表O(n + e)，n为顶点，e为边

📒 从题中的总结

• 图的深度优先遍历 可以 适用于无向图

网

• 边或弧带权值的图

• 两个顶点无边，使用∞表示。

  

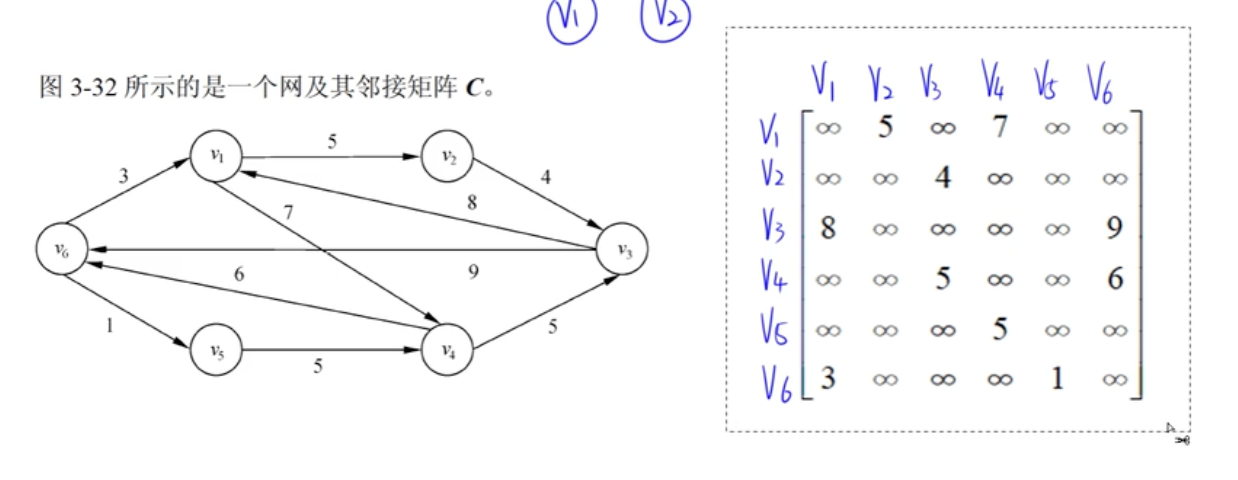
拓扑排序

• AOV网，顶点表示活动，有向边表示活动之间优先关系。优先➡️下一级

• AOV是有向无环图，有环会有逻辑矛盾

• 拓扑排序

  

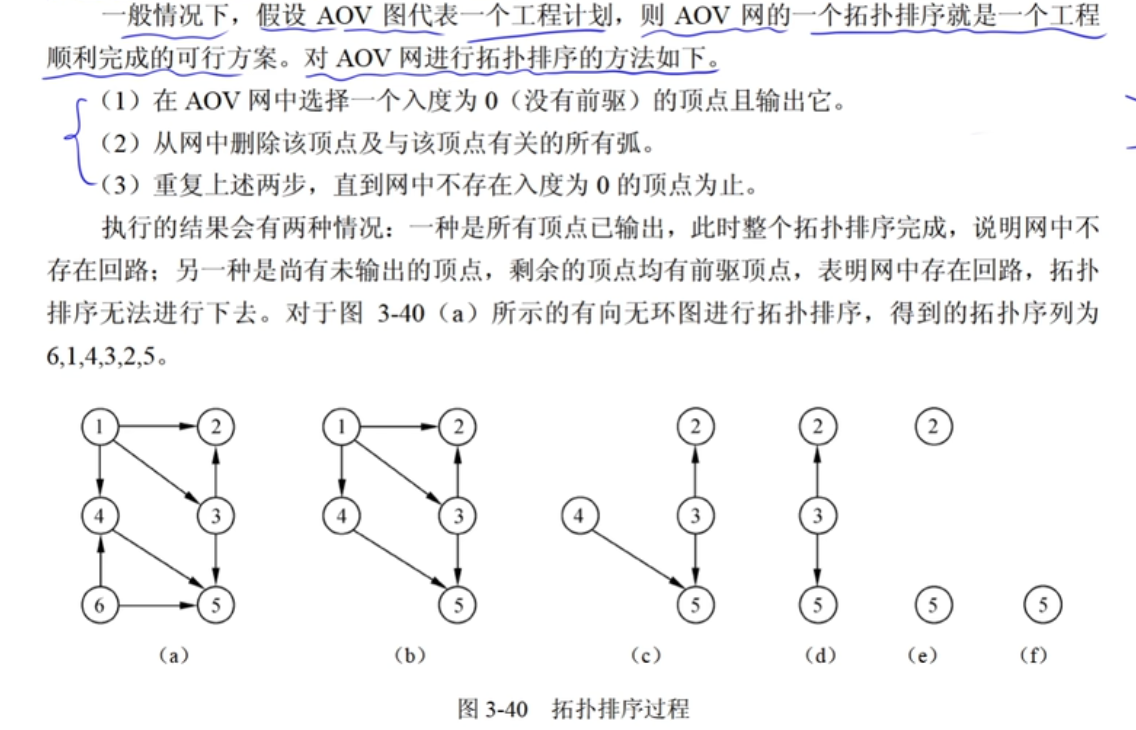
​ 顶点vi在vj之前，可能存在<vi, vj>，一定不存在<vj, vi>的路径

查找

• 静态查找表
  • 查询是否存在
  • 检索数据元素特性
  • 顺序查找、折半查找、分块查找
• 动态查找表
  • 插入
  • 删除
  • 二叉排序树、平衡二叉树、B_树、哈希表
• 关键字：标识数据元素。主关键字：唯一标识；次关键字：能标识多个数据元素（不唯一）

顺序查找

• 从头开始依次比较，相同则为成功
• 长度为n，顺序查找成功的平均查找长度为：(n + 1) / 2，通过等比推导
• 既适用于顺序存储结构，也适用于链表结构

折半查找（二分）

• 最多比较的次数：min(log₂n) + 1
• 要求顺序存储，有序排列
• 做题注意题目是否已经指定取整方式

哈希表

• 哈希表通过计算一个以记录的关键字为自变量的函数，来得到该记录的存储地址。通过值获取位置

• 哈希的冲突是无法避免的

• 哈希函数的构造方法

  • 哈希函数应是一个压缩映像函数，应具有较大的压缩性，节省存储空间

  • 应具有较好的散列性，尽量避免冲突

  • 对关键字进行计算，尽可能使关键字所有组成部分都能起作用

  • 直接定址法、数学分析法、平方取中法、折叠法、随机数法、除留余数法

  • 解决冲突的方法：

    • 线性探测法：冲突后，+1直到不冲突
    • 二次探测：冲突后根据序列进行加减 1,-1,4,-4,9,-9
    • 链地址法

    

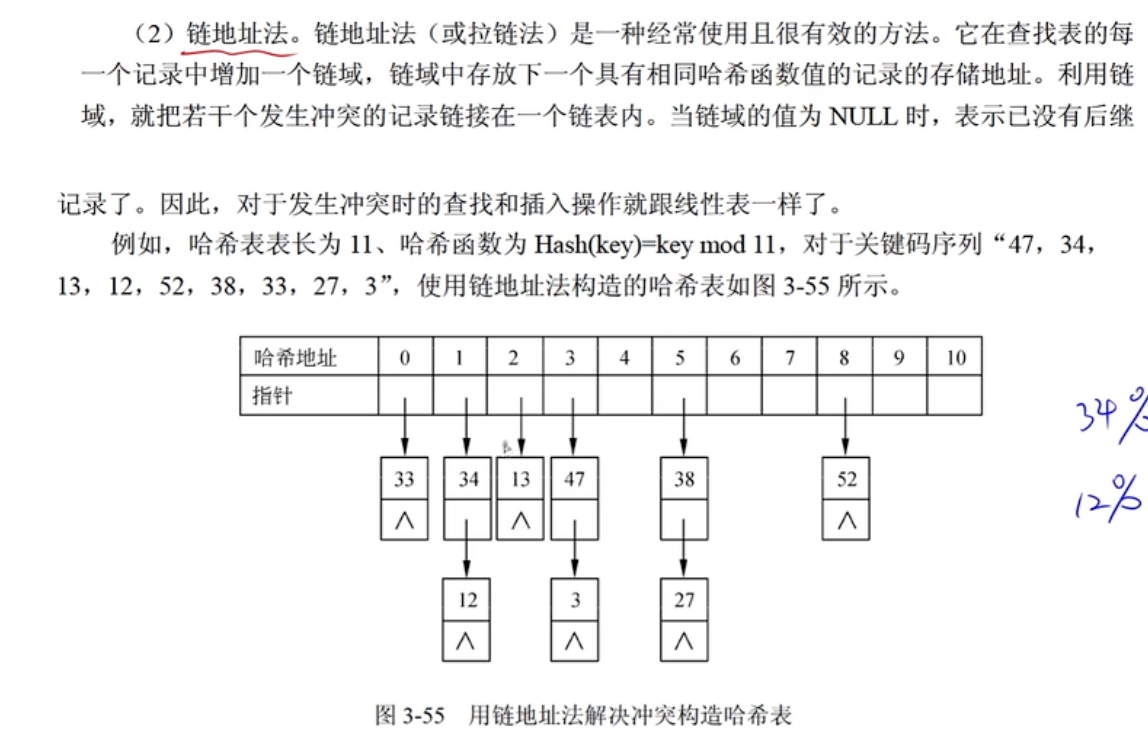
• 哈希表的查找

  • 查找过程中比较关键字的个数取决于 哈希函数、处理冲突方法、哈希表装填因子
  • 装填因子定义：表中装入的记录树 / 哈希表的长度
  • 装填因子越小，发生冲突可能性越小

堆

小顶堆、大顶堆

• 可以用树表示，小顶堆：父小于子；大顶堆：父大于子

排序

• 排序稳定：对于两个相同的值，排序后顺序依然一致。

• 算法

  

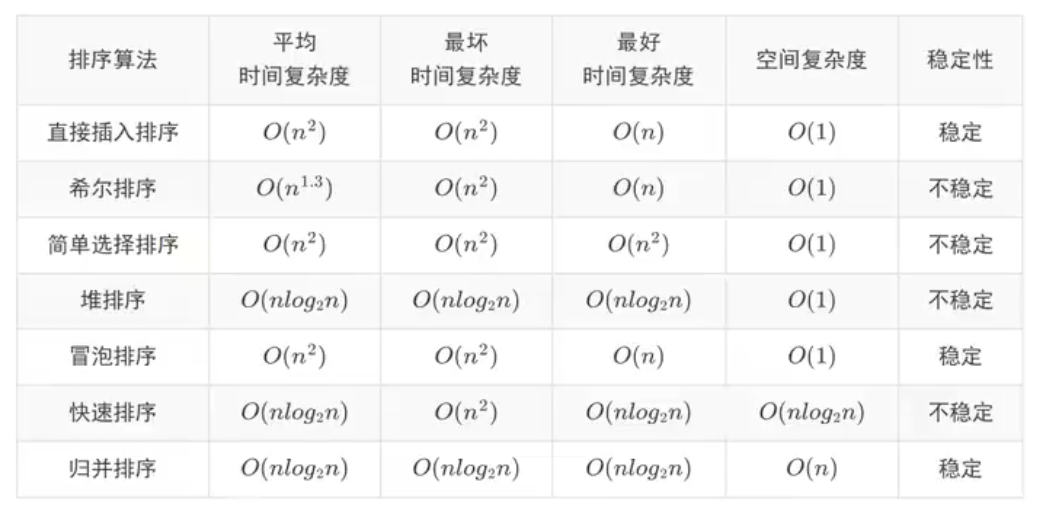
直接插入排序

• 每当新插入一个时，依次去做比较。打扑克的排序
• 适合于基本有序的数组进行排列

希尔排序

• 直接插入排序基础上优化，先分割为子序列，进行排序，最后进行总体排序

计数排序

• 统计每个数的数量，再根据数量按照序列还原序列。
• 适用于关键字数量少（例如只有0-9）的情况

简单选择排序

• 先遍历找最小的值，放到第一个（默认第一个是最小，遍历完有更小的就交换）。再对后续的数组进行同样的处理。

堆排序

• 每次排序都可以确定一个元素的最终位置
• 新建堆 ➡️ 初始化大/小根堆 ➡️ 层序遍历（有序的，递增/递减）

冒泡排序

• 通过重复比较相邻元素并交换位置，将最大（或最小）元素逐步“冒泡”到数组末尾的简单排序算法
• 每一次循环都可以将最大/小值冒泡到最后，每次循环长度都在-1

快速排序

• 步骤
  • 选基准：从数组中选一个元素作为基准（通常选第一个或最后一个）。
  • 分区：将数组分为两部分，小于基准的放左边，大于基准的放右边。
  • 递归：对左右两部分递归执行上述步骤。
  • 合并：递归结束后，数组自然有序。
• 基本有序的序列是最坏的情况

归并排序

• 算法设计方法：分冶法

📒 从题中的总结

• 优先队列采用堆数据结构实现，堆的插入时间复杂度是O(lg n)